Reading on Refraction Part II

The Refraction of Light, Part II

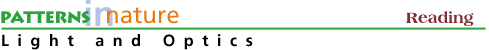
The Refractive Index

The ratio of the velocity of light in vacuum to the velocity of light in a medium is referred to as the medium's refractive index, denoted by the letter n. The velocity of light in a vacuum is 3.0 x 10⁸ m/s or about 186,000 miles/s. If we go back to our beach/ocean analogy we can think of the refractive index of the water as something like its density. Air is not very dense at all (its refractive index is 1.0003), so the people run through quite easily; but when they run into water, which is denser than air (and has a refractive index of 1.333), the people slow down and their line bends at the ocean/beach interface. For light, the index of refraction n equals the ratio of the velocities of light in vacuum (c) to that in the medium (v), that is n = c/v.

Refractive indices are most easily determined from the measured values of the incident angle and the angle of refraction and their geometric relationship. Values of the refractive indices for the media shown in Fig. 2 are given below.

Values of Refractive Index

Medium	Refractive Index
Air	1.0003
Water	1.33
Linseed Oil	1.48
Co Green	2.00
Diamond	2.42
Ti White	2.5

The path of light in air incident on and transmitted through a glass plate is shown in Figure 5. The angle of the incident ray to the normal is 45° and equals that of the reflected ray. The transmitted ray is refracted at an angle of 28° to the normal and exits the glass at an angle of 45° to the normal, an angle equal to that of the incident ray. This explains why, for example, the image we see through a flat-glass window pane is unchanged from that seen through an open window.

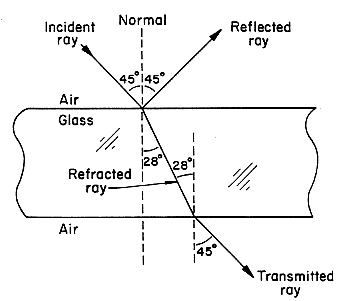
Figure 5. Light incident on a glass plate. The reflected part of the ray is shown along with the light path for the refracted component.

Light incident normal to a glass plate does not change direction as the transmitted light continues normal to the surface (air/glass interface). The light is not refracted (that is, no change in angle) but the wavelength and velocity do change. Light does reflect as it encounters the air/glass interface (about 4% in this case).

The paths of light traversing different media are reversible. The same relations are obeyed in Fig. 5, for example, if the light were incident on the bottom of the glass plate. Similarly, in Fig. 4, if the light started in the water, it would be refracted at the water/air interface and would retrace the same reversible path as for light incident from air.

Total Internal Reflection

If light is inside a material such as glass with a larger refractive index n₂ than that n₁ of the material outside such as air, there is an angle, the critical angle of incidence, beyond which the light is reflected back into the material and does not escape. This is total internal reflection. The critical angle i_c is given by

sin i_c = n₁ / n₂

For light exiting glass, n₂ = 1.5, the relation becomes

sin i_c = 1.0 / 1.5

and the value of the critical angle of incidence is 41°. Light in glass at any angle of incidence to the normal 41° or greater will be reflected from the glass-air interface back into the glass. The bluer area in Fig. 6 is the angular region where light is reflected back into the glass. The greater difference in the two indices of refraction, the smaller the amount of light can escape.

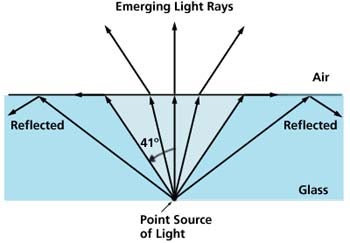
Figure 6. The internal reflectance at an air/glass interface for light rays from a point source in glass. Light rays incident at angles to normal at greater than the critical angle (here, 41° for glass to air) do not leave the material and are reflected at the glass/air interface.

Light fibers and diamonds are both materials with a high refractive index and are used for their properties of "retaining" light.

Chromatic Aberration

Fortunately, the index of refraction of most materials is not the same for each wavelength passing through it; otherwise, we wouldn't see rainbows or the sun's green flash at sunset. When white light passes through a lens or a prism, blue light is bent more than red light. When seen through a lens, this change of index of refraction with wavelength is called chromatic aberration, the change in focal length for different wavelengths of light.

Figure 7. Chromatic aberration in a lens. Blue light is bent more than red light so its focal length is shorter than that of red light, and the "blue" image is located in front of the "red" image.

In precision lens systems, chromatic aberration is undesirable, so achromatic lenses are used to reduce or eliminate this effect. The simplest achromatic lens system is just two lenses with different indices of refraction put together: one convex, one concave. Quality telescopes, microscopes, and camera lenses all have achromatic lens elements.

Return to the First Page of the Refraction Readings.