Reading on Refraction

The Refraction of Light

Changing the Speed of Light

Ever notice how your leg looks bent as you dangle it in the water from the edge of a pool? Why do fish seem to radically change position as we look at them from different viewpoints in an aquarium? What makes diamonds sparkle so much?

These are all questions that can be addressed with the important concept of refraction, the bending of light as it encounters a medium different than the medium through which it has been traveling. This meeting place of two different media is called the interface between the media. All refraction of light (and reflection) occurs at the interface.

What happens at the interface to make light refract or reflect? When light is incident at a transparent surface, the transmitted component of the light (that which goes through the interface) changes direction at the interface. Another component of the light is reflected at the surface. As shown in Figure 1, the refracted beam changes direction at the interface and deviates from a straight continuation of the incident light ray.

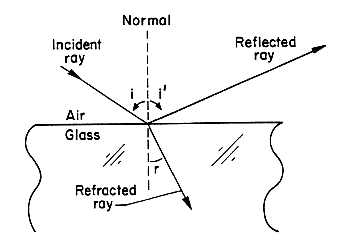
Figure 1. Light in air incident on glass surface where it is partly reflected at the interface and partly transmitted into the glass. The direction of the transmitted ray is changed at the air/glass surface. The angle of refraction r is less than the angle of incidence i.

The change of direction of light as it passes from one medium to another is associated with a change in velocity and wavelength. The energy of the light is unchanged as it passes from one media to another. When visible light in air enters a medium such as glass, the velocity of light decreases to 75% of its velocity in air and in other materials the decrease can be even more substantial. For example, in linseed oil, the velocity decreases to 66% of its velocity in air. Figure 2 displays in bar chart format the velocity of light in different media. The 100% value is the velocity of light in vacuum. For air, the velocity is 99.97% of the speed in vacuum. For some pigments such as titanium (Ti) white, the velocity decreases to 40%.

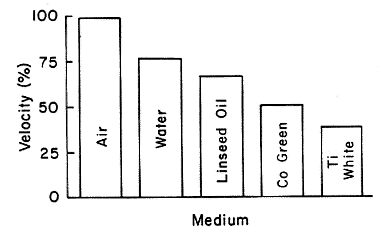
Figure 2. Bar chart of the velocity of visible light in different media. The value of 100% refers to the velocity of light in vacuum.

Waves

Refraction is an effect that occurs when a light wave, incident at an angle away from the normal, passes a boundary from one medium into another in which there is a change in velocity of the light. Light is refracted when it crosses the interface from air into glass in which it moves more slowly. Since the light speed changes at the interface, the wavelength of the light must change, too. The wavelength decreases as the light enters the medium and the light wave changes direction. We illustrate this concept in Figure 3 by representing incident light as parallel waves with a uniform wavelength

. As the light enters the glass the wavelength changes to a smaller value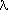

'. Wave "a" passes the air/glass interface and slows down before b, c, or d arrive at the interface. The break in the wave-front intersecting the interface occurs when waves "a" and "b" have entered the glass, slowed down and changed direction. At the next wave-front in the glass, all four waves are now traveling with the same velocity and wavelength

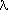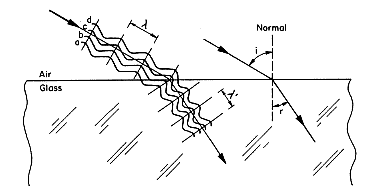
Figure 3. Light waves of wavelength

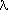incident on glass change direction and wavelength when transmitted into the glass.

The waves are continuous and remain connected as they pass from one medium to another. We can think of it like a long line of people running into the ocean. As the first few people run into the water, they're slowed down because it's harder to run in water. Thus, they bunch up and stay bunched up as they run through the water. When everyone in the line has entered the water, we would see a line of people all running in the same direction, but the line would be shorter and the people would be bunched close together. If they run back to the beach, the first few people would clear the water and run faster. Eventually everyone will have cleared the water and would be running at the original pace with the original spacing between persons.

In this analogy we can think of the whole line of people as the "light wave" and the people themselves as the "crests" of the wave. The distance from one person to her neighbor would be the wavelength of the wave and the water would be the medium into which the light wave is traveling. Why, then does the light wave change direction when it enters the new medium?

We can extend our analogy and imagine two lines of people running into the ocean from the beach. The lines are close together and each person in a line is matched up with another person in the other line. This is analogous to waves a, b, c, and d in Fig. 3 above. When line "a" hits the water first, the line slows down. In order to maintain the one-to-one relationship with the other line, both lines must turn when they hit the water. Which way do they turn? Towards the normal - the imaginary line that runs perpendicular to the interface between the two media (the water and the beach); a pier is a good example of something normal to the water/beach interface.

So the two lines must turn towards the normal when they hit the water. The greater the change in velocity and wavelength, the greater the change in direction. Figure 4 shows the change in direction for light in air incident at 45° on water with refracted angle of 32° and on titanium white (a paint pigment) with a refracted angle of 16°. These angles correspond to the differences in velocity shown in Fig. 2.

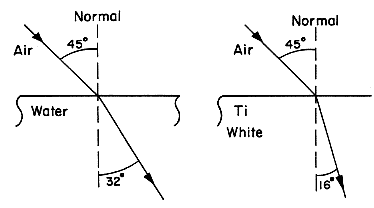
Figure 4. Light incident at 45° on water and Ti white. The angles of refraction (32° for water, 16° for Ti white) depends on the optical properties. The reflected components are not shown.

We can characterize the change in velocity by a number called the refractive index of the material.

Continue the Refraction Reading.