Rainbow Reading 4

Rainbows, part IV

Gravity's Rainbow

Here's the scenario: we have a block of raindrops in the sky being illuminated by the sun, refracting and dispersing the light into its various colors, and reflecting those colors back. An important thing to notice is that the red light gets reflected back at 42° from our antisolar line, and the blue light gets reflected back at about 40° from our antisolar line.

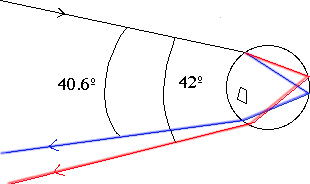
That is, every raindrop 42° of the antisolar line is reflecting red light back to our eyes. If we look at every raindrop that is 42° from this line, we would see a circle of raindrops centered on the line.

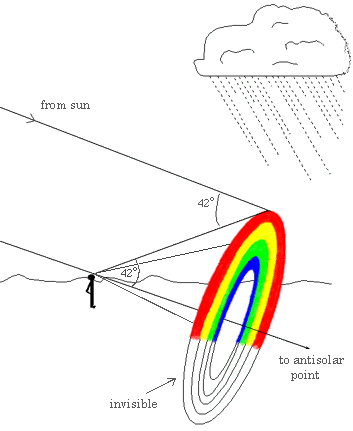
Unfortunately, the horizon gets in the way of most of the rain, so we only see an arc or a bow; however, from the vantage point of a mountain-top or an airplane, full rainbows can be seen on cloud layers below.

Rainbows in 3D

Remember that rain is not falling in a flat sheet, but in varying distances from you. This causes the "rainbow circle" to be formed at varying distances. What shape is made by circles at varying distances from an apex (in this case, your eye)?

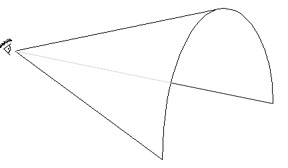
We find that the raindrops that contribute to your rainbow all lie on a cone with its apex at your eye. So when you are looking at a rainbow, you are looking at the collected light from many many raindrops which, for a fleeting moment, collectively produce a "cone of color" with its apex at your eye. If you move to the left or the right, your are looking at new raindrops, and hence, a new rainbow!

If you are admiring a rainbow with a friend, you are both seeing different rainbows.

Each rainbow is your own.

"..I once saw two rainbows in the sky. How did that happen?"

Why is the sky brighter inside the rainbow?