People find it cumbersome to speak of units of measurement like "one ten thousandth of a billionth" of an inch, or even "ten to the minus thirteenth" (10^-13) inches; so they devise different names. No one gives the distance between cities in inches; we use miles. For people's heights we use feet and inches. But there are 12 inches in a foot, 5280 feet in a mile and so on. That gets messy if we want to convert from miles to inches. It is easier to use the metric system where everything goes by powers of 10:

	1 meter          = 1 m  = 1 yard
	1 kilometer      = 1 km = 103 m  ~ 5/8 mile
	1 centimeter     = 1 cm = 10-2 m  ~ 2/5 inch (width of a pen)
	1 millimeter     = 1 mm = 10-3 m  ~ 1/25 inch (width of lead in pencil)

This much is fine for everyday lengths, but for light we have to use even smaller units of length because its wavelength is so small. Unfortunately, many different names are used. The wavelength of yellow light in vacuum may be called 5750 Å or 575 m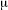 or 575 nm or 0.575 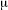m. The units used here are:

	1 Å  =  1 Ångstrom  = 10-10 m

(This unit is often used because a typical atom is a few Ångstroms in size.)

	1 nm  =  1 nanometer  =  10-9 m
		(formerly written 1 m)
		
	1 m  =  1 micrometer  =  1 micron  =  10-6 m

(This is a convenient unit for high-power microscopes, with which one can look at objects as small as a few micrometers. 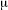is the Greek letter "mu")

There is a method to the prefixes centi-, milli-, etc. They multiply the unit by some power of 10. For example, milli- always means one thousandth. The important prefixes are:

	n  =  nano-  (Greek "dwarf")  =  10-9 (thousand millionth)
	  =  micro-  (Greek "small")  =  10-6 (millionth)
	m  =  milli-  (Latin "thousand")  =  10-3  (thousandth)
	k  =  kilo-  (Greek "thousand")  =  103  (thousand)
	M  =  mega-  (Greek "big")  =  106  (million)

Thus we can now proudly state that 1 nm = 10^-3 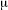m.

Scientific Notation:

indentAstronomy is the subject of very large numbers. Microscopy is the subject of very small numbers. Consequently, scientific notation has been introduced to deal with such quantities. For example, the distance from the Earth to the Sun is referred to as the Astronomical Unit (AU) and is:

1 AU = 150,000,000 km = 1.5x l08 km = 9.2 x lO7miles

indent Another dimension to illustrate this kind of notation is the mass of the Sun expressed in units of kilograms (kg):

Mass of the Sun = 1 Solar Mass = 2.0 x 1030 kg

indent Note that 2.0 is the coefficient and 30 is the exponent. Not only can one use scientific notation to express large numbers but also very small numbers. For example, the size of an atom is on the order (or about) a few Ångströms (Å) which is defined as:

1 Ångström = 1 Å = 1.0 x 10-10 m = 0.0000000001 meters

indent aNote that the negative sign in the exponent means the value is less than one.

indent Here are some alternate forms of notation for the same numerical values:

3.2 x 108 = 32 x 107 = 320 x 106 = 320,000,000 = 320 million

0.0002 = 2 x 10-4=20 x 10-5= 200x10-6

indent Using a pocket calculator with an exponent key, usually labeled EX or EE or EX, the number: 4.3 x 10⁵ is entered as 4.3 EX 5.

Examples of Scientific Notation, Metric Prefixes, and Symbols

Word	Sci. Notation	Metric Prefix	Symbol
one billionth	1 x10-9	nano	n
one millionth	1 x I0-6	micro	µ
one thousandth	1 x 10-3	milli	m
one	1
one thousand	1 x 103	kilo	k
one million	1 x I06	Mega	M
one billion	1 x 109	Giga	G
one trillion*	1 x 1012	Tera	T

*in American English, 1 x 10¹² = one thousand million in British English.

Examples of simple matlh using scientific notation:

Addition:

3.2 x 108 + 0.40 x 108 = 3.6 x 108

Subtraction:

4.52 x 105  - 3.32 x 105 = 1.20 x 105

Multiplication:

 (3.2 x 10-8) x (2 x 104) = 6.2 x 10-4

Division:

 (3.2x 108) / (2 x 10-4) = 1.6 x 10 12 

aaaaaNote that when you multiply, the coefficients are multiplied together while the exponents (or powers of ten) are added. Similarly, when you divide, the coefficients are divided and the exponents are subtracted.

^* Seeing the Light, D. Falk, D. Brill, D. Stork, J. Wiley & Sons, New York

Complete the Powers of 10 Activity