 |
2D
UNIT V: SCALE |
To understand and apply scale, proportion, and grids as they relate to the two-dimensional picture plane.
------------------------------------------------
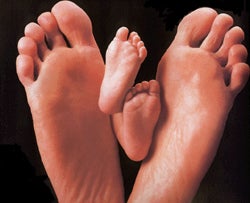
How big are your feet? If you describe them as simply "large" we still don't know how much bigger your feet are than the general population's. Are they the size of an average sized adult's, the size of a basketball player's, or the size of two small canoes? The point is this: size is only meaningful insofar as it tells us something about an object's dimensions in relationship to other things.
 |
Diane Arbus, A Jewish giant at home with his parents in the Bronx, N.Y. 1970 |
In the examples above, we understand the differences between "small" and "large" due to a comparative relationship.
Rather than endlessly comparing one thing to another, most cultures agree on systems of measurement that help to establish clear dimensions of an object. A person is so many feet or centimeters tall. A horse is so many hands high. A highway is so many miles or kilometers long. In Japan, a room's size is described as accommodating so many tatami mats. By making either a mental comparison between a given object and a given dimension, or actually taking a measurement of something, we can move with relative ease between actual things and abstract systems of measure.
|
A traditional Japanese room |
Tatami mats stacked and drying in the sun |
Tatami mats are usually three by six feet and made of tightly woven rice-straw pads from 1 ¾ - 2 ½ inches thick. They are covered by finely woven mat on top, edged with cloth. Rooms are built to contain a certain number of these usually three by six foot mats, and the size of the room is referred to by the number of mats. A four and a half mat room, for example, would be nine by nine feet. A formal Japanese tea room is four and a half mats. http://www.japanesespaces.com/components.html
Once we have measured something, we can play with its scale. Scale is another relative term meaning "size" in relationship to some system of measurement. While we can speak generally of things that are "large or small in scale," in art and design when discussing scale we are referring to the size of object in relationship to a clear set of measurements. For example, if you tell me that the shoes you just drew are "half scale," I would assume that they were half the length of the actual object--that is, one-half "full" or "actual size."
 |
The little canoe on the left is called a "salesman's model" because the salesmen for historic Maine canoe companies used to carry scale models of their company's offerings. The "half scale" model is an exact representation of the "full size" 17 foot canoe at the right. |
When we move into some of the design professions, like architecture or industrial design for instance, other conventions apply. For example, if I said I want a drawing in "1/4 scale"*, generally I mean that I want a drawing in which "1/4 inch equals 1 foot." In this case, instead of measuring the actual object against a system of measurement, we are relating two sets of measurements.
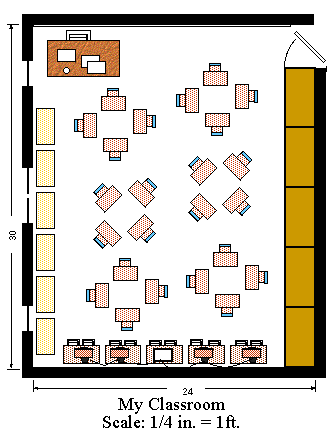
*http://www.nycenet.edu/oit/math-kitecture/what.htm
One of the particular challenges in moving between scales is to understand the difference between the scaling of something in "linear measurements" versus "area measurements." In general, the conventions of 2D design dictate that we utilize linear measurements to "scale up" or "scale down" a graphic image. We would only need the corresponding dimensions of the original and the desired reduction--height, for example--to determine the scaling factor. If an original drawing is 4 inches in height, and the reduced image is to be 2 inches, the scaling factor is .50 (50%). [2 inches divided by 4 inches equals .50]. This scaling factor (.50) could be applied to any aspect of the associated graphics that required reduction.
 |
|
The image on the left is 4 inches high. The image on the right is 2 inches high--it has been scaled by .50 (4 inches x .50 = 2 inches) |
If one assumes that an object should be scaled by virtue of its total surface area, we arrive at an entirely different outcome. The final image would have to be calculated by gridding the entire surface of the drawing, then creating a proportionally accurate grid that occupied 50% of the total area. If the original were 12 square inches(4" x 3"), for example, a reduced drawing based on area would be 6 square inches (~2.1213" x ~2.8284")
|
Fig. A |
Fig. B |
Fig. C |
Proportion refers to the ratio between the parts of a larger whole. If we go back to the shoe example for a minute, a drawing--at virtually any scale--that represented the shoes in "correct" proportion would show the actual relationship of height, width, and depth. I could alter the scale of the object without changing the proportions. Or, if I wanted to exaggerate the proportions (like a circus clown might do), I might make the length of the shoes twice the length of the original shoe and preserve the height and the width. In so doing, I have changed the proportions of the object--that is, I have changed the ratio of the parts describing the whole. If the original ratio of height, width, and depth could be represented by the following expression: 1:1:1, the "new" clown shoes could be represented by 1:1:2, where the 2 represents the new exaggerated "depth" (or length). "Ideal" proportions reflect the taste and goals of particular communities. For example, among dog breeders, there are ideal ratios governing the proportions of a dog's body such as the length of a dog's legs to the height of its upper body.
 |
 |
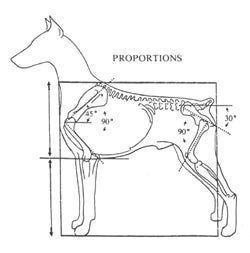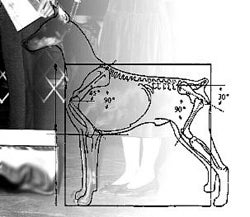http://www.blast.net/chili/Sizeprop.html
A
grid is a system of fixed horizontal and vertical divisions. Anything,
no matter how complicated or irregularly shaped, can be conceived of in
terms of X (horizontal) and Y (vertical) axes. The mechanical regularity
of a grid can be useful in determining relationships between the parts
of a painting or other graphic work (a map for instance). A grid can also
be a useful tool for translating a given image from one scale to another
(see "Using Grids for Scale Translation")
or altering the proportions of an image.
Sometimes scaling operations are represented by changes in percent of the X, Y (or Z in 3D) axes. For example, imagine a drawing of the outline of a house in which the height and width are equal. If you were to change the X axis to 25%, the house would be 1/4 its original width. If you were to change the Y axis (vertical) to 200% of its original size, the house would be twice as tall. By changing both the X and the Y axes, you could transform the house into what looks like a tower!
 |
|
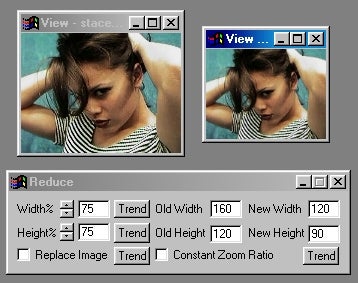
In the example above, computer software is used to change an image to 75% of its original size. Note that 120 pixels wide is 75% of the 160 pixels wide of the original. In 2D work, linear measurements are used when scaling between dimensions.
http://www.blackbeltsystems.com/html_docs/f_op_reduce.html#ient1796
It's probably clear by now that you needn't scale the X and the Y axes equally. Not only that, you needn't maintain the "orthogonal" (i.e., the 90 degree relationship between horizontal and vertical) either. Things get pretty interesting when you consider grids that are set into oblique perspective or translated into wave patterns, for example. Try experimenting with projecting an image onto unexpected shapes or surfaces.
We will be discussing grids again in the Unit on Compositional Strategies--this time as an aid to graphic layout.
A further variation on the concept of proportional shifts is the idea of "anamorphosis." Anamorphosis--literally "against form"--was explored by artists as early as the late 15th century. It is predicated on the idea of a viewer observing a picture plane from an oblique angle
Bicycle image is seen as
normal from the perspective
of a bicyclist.Same image seen from
above. Note how bicycle
image is stretched vertically.
One of the most famous examples of anamorphosis was done by the Dutch artist, Hans Holbein, in the early 16th century in a work called "The Ambassadors."
Scale and Proportion in flower arrangement. http://www.hort.vt.edu/faculty/McDaniel/hort2164/R4ScaleProportion.htm
Mathematical concepts. http://www.etsimo.uniovi.es/hypgraph/design/composition/scale_and_proportion_in_composit.htm
Scale and Proportion in Architecture. http://www.artinarch.com/ct18.html
ASSESSMENT