To understand and apply various methods of composing the two dimensional picture plane
------------------------------------------------------
While you have used grouping or unity principles in Unit III (Unity) to focus attention and move the eye across the picture plane, we are now going to explore several methods for creating effective overall 2D compositions.
Balance--the equal distribution of visual "weight"--is a feature of many effective compositions. Imagine a balance beam--like a seesaw--with a fulcrum at its midpoint. As you know, two objects of equal weight, placed at opposite ends of the beam, will achieve equilibrium across the two sides of the beam. Similarly, a composition can be balanced by adjusting the distribution of "weight" across the picture plane. This balance can be achieved in many ways.
In the diagram above, various methods of dividing the picture
plane are illustrated. These can be an aid to establishing an
underlying compositional structure before beginning to work with
specific imagery. Radial symmetry can be used to create "multi-symmetrical" compositions that have
a strong visual center of interest and a high degree of optical
energy. Radiation patterns include (see illustrations below from
upper left to lower right): centrifugal (radiating from inside to outside--like a starburst), concentric (target like forms), spiraling (iris and nautilis shapes), centripetal (radiating from outside to inside) patterns.
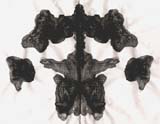The most straightforward method is to distribute elements equally
on both sides of an imaginary center line by repeating or reflecting
shapes from one side onto the other. This vertical "mirroring"
is called symmetry. An inkblot is a perfect example of a symmetrical composition--that is, a
composition that repeats the same elements on both sides of a
central vertical axis. (It should be noted that while the elements
are not "identical"--they are "left hand and right hand versions"
of one another--the result constitutes perfect "symmetry" nonetheless.)
The use of asymmetry can result in compositions that are still "balanced" as far as
visual weight. The difference is that elements such as value,
color, shape, texture, and line are used in varying combinations
to achieve that balance. For example, in this turn of the century
poster, the high contrast and detail of the text set against the
black shape is an effective counterweight to the visual interest
and foreground position of the lightbulb. Note also the repetition
of the yellow gold color and the subtle detail of the company
name being repeated in the filament of the bulb.
Further examples of asymmetrical composition: In the image on
the left (above), the smaller black dot, because of its intense
contrast to the background, easily balances the larger white square.
This is balance using value and size. On the right, the large
pink sphere is balanced against the small green square (which
is even more optically charged because of the reddish brick background).
This is balance by color.
Another compositional strategy includes "allover" composition or "crystallographic" balance where equal emphasis is given to every area of the picture plane. Examples of this range from Jackson Pollack's allover drip paintings to simple checkerboard patterns where every square is identical.
Finally, there are mathematical systems for determining "perfect proportion" and balance that date back to the ancient Greeks. One of the most famous systems is that of the Golden Section.
What is The Golden Section? The golden section is a line segment
divided into two parts. Point C is positioned such that the ratio
of the short half to the long half is equal to the ratio of the
long half to the whole. Symbolically:
A------C---B where CB / AB = AC / AB, or AB^2 = BC x AC
This relationship can also be expressed as 1:1.618033 where 1 equals the height of the rectangle (A----C).
Mathematics aside, from this "ideal" ratio, all manner of proportional systems have been derived. One beautiful example is the Golden Spiral which shows the same ratio above applied to stairstepping boxes--each box being .681 percent of its neighbor. This sequence of spiraling boxes is traversed by a series of gradually diminishing tangent arcs. The arcs combine to create a spiral--the properties of which echo many forms in the natural world--including the chambered nautilus sea shell and many plant forms.
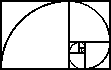
Golden Spiral
Many painters, architects, and musicians have used the principles of the Golden Section to determine relationships between the compositional elements of their work. For example, the architect Andreas Palladio utlized the Golden Section in determining the layout of the facades of many of his famous cathedrals in 16th century Italy. And the ancient Greeks used the ratio of height to width of the Golden Rectangle (a rectangle whose height is the square root of 5 times its width) to determine the proportions of the facade of the Parthenon.
Related to the ratios of the Golden Section is the Fibonnaci number progression (1,1,2,3,5,8,13,etc). See the following page for numerous radially symmetrical designs by Edward S. May based on this progression.
Edgar Degas; Dorothea Lange; Rene Magritte; Edward S. May; John Szarkowski; Leonardo Da Vinci;
McCollum, Allan. interview, Arts Magazine (1985)
Szarkowski, John,
--Mirrors and Windows: American Photography Since 1960 (1978).
--American Landscapes (1981).
--The Works of Atget, 4 vols. (1981 - 85).
Identity Protest and Persuasion Technology Collaboration Other Voices Art for Hire Fantasy The Natural World Spirit Worlds
A.
B.
C.
D.
E.
F.
G.
H.
I.
J.
Mining for Ideas